八数码问题
实验说明
使用 A∗ 算法求八数码问题。给定初始局面和目标局面,动态演示求解方案。
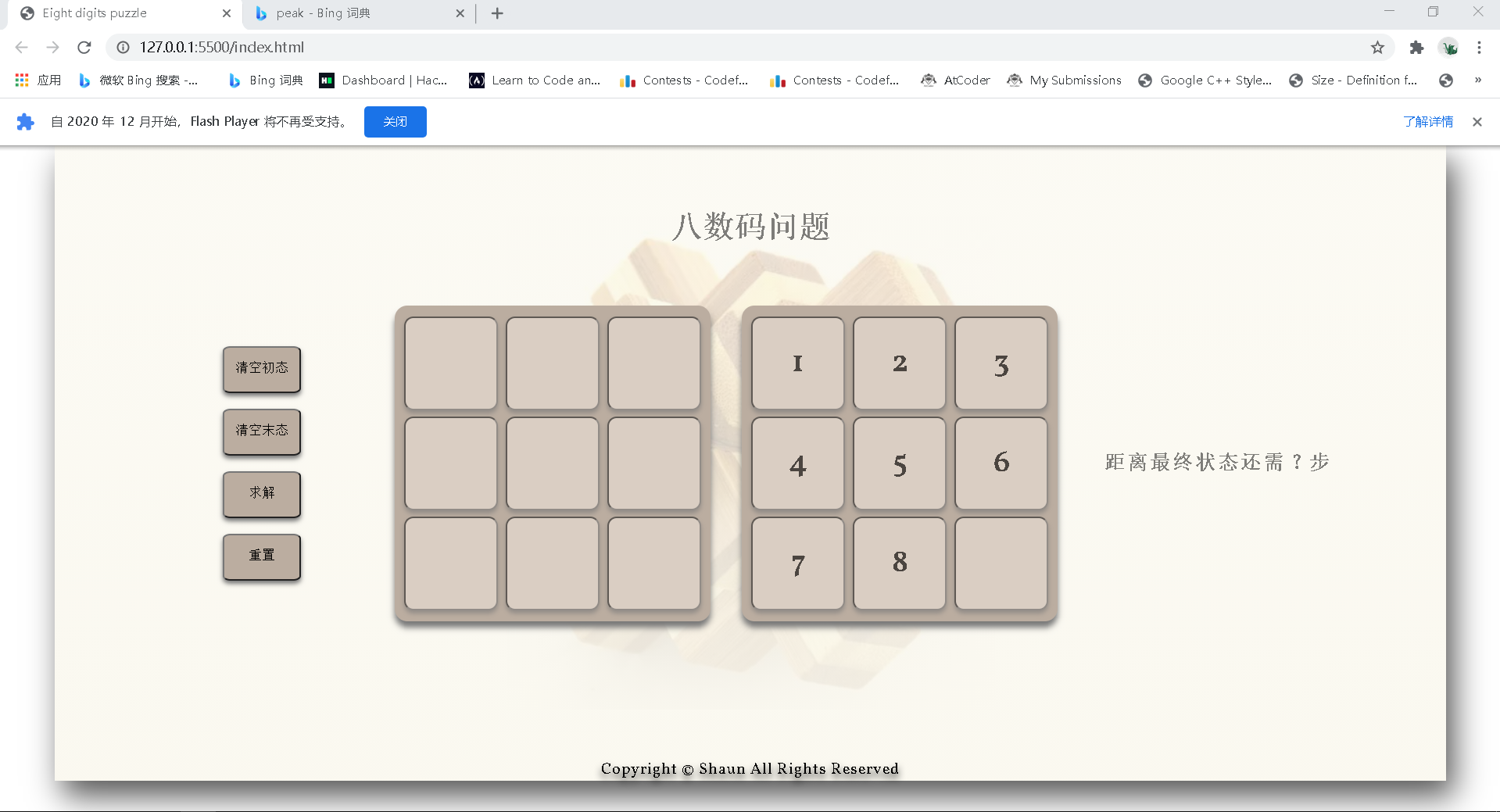
由于之前使用过 c++ 求解八数码问题,本次实验采用的是 javascript 求解,并通过 html + css 进一步实现交互界面。效果如下:



算法分析
求解八数码问题有很多方法,比如深度优先搜索、宽度优先搜索、一致代价搜索、双向搜索。其中深度优先搜索容易在较深的分支上停留很长时间,对于目标远离初始搜索分支的搜索树来说,效率是极低的; 宽度优先搜索对搜索树进行层次遍历,但是当子树极度不平很时,搜索效率也是相对较低的。
总的来说,上述无差别的搜索是不太合理的,在进行搜索时很多情况下是在找不到解的路线上进行搜索。因此我们希望通过一些启发方法,能最大可能地在有最优解的路线上进行搜索,这就是 A∗ 算法所做的。
在分析 A∗ 算法之前,先回顾以下优先队列 BFS 算法。该算法维护了一个优先队列,不断从堆中取出当前代价最小的元素进行扩展。每个状态第一次从堆中取出时,就得到了从初态到该状态的最小代价。然而这样的策略不是完善的,当前搜索代价小可能会导致未来搜索花费更大的代价;当前搜索代价大,被扩展地晚,最终的代价可能更优。
为了提高搜索效率,可以对未来可能产生的代价进行预估。在搜索时,仍然维护一个堆,不断从堆中取出当前代价 + 未来估价最小的状态进行扩展。
在八数码问题中,当前代价即为空格已移动的次数。
对于未来估价,由于未来估价不能大于未来实际代价,这里采用所有数字在当前状态 state 中的位置与目标状态 end 中的位置的曼哈顿距离之和,因为每次移动空格只会有一个数字位置改变,一个数字移动到目标状态的一定至少需要移动两位置的曼哈顿距离。即:
f(state)=num=0∑8(∣statexnum−endxnum∣+∣stateynum−endynum∣)
算法设计实现
根据上述分析可设计 javascript 估值函数:
1
2
3
4
5
6
7
8
9
10
11
12
| function evalute(curStep) {
let res = curStep;
let curx = new Array(9), cury = new Array(9);
let endx = new Array(9), endy = new Array(9);
for (let i = 0; i < 3; i++)
for (let j = 0; j < 3; j++) {
curx[array[i][j]] = i, cury[array[i][j]] = j;
endx[endArray[i][j]] = i, endy[endArray[i][j]] = j;
}
for (let i = 0; i < 9; i++) res += Math.abs(curx[i] - endx[i]) + Math.abs(cury[i] - endy[i]);
return res;
}
|
为了保证 A∗ 算法的效率,每个状态只需要在第一次被取出时扩展一次。本题由于总共有9个格子,故可用每个状态可用 9 位数字进行简单表示(不舍弃前导零)。对于 c++,可以将这些数字放在 std::unordered_map<T, T> 或 std::map<T, T> 中,在 javascript 中可以用其提供的 Map() 来存放键值对。当然还可以通过其它方法优化状态的记录,在后面的优化内容中会提到。
去重相关代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| function _hash() {
let res = 0;
for (let i = 0; i < 3; i++)
for (let j = 0; j < 3; j++)
res = res * 10 + array[i][j];
return res;
}
if ((dis.get(nxtBoard.hashVal) == undefined) || dis[nxtBoard.hashVal] > dis[curBoard.hashVal] + 1) {
dis.set(nxtBoard.hashVal, dis.get(curBoard.hashVal) + 1);
pre.set(nxtBoard.hashVal, curBoard.hashVal);
q.queue(nxtBoard);
}
|
在 $A^* $ 搜索函数中,我使用的是优先队列宽度优先搜索。由于本次实验重点在于 A∗ 算法与求解方案,故使用的是 npm 包中的优先队列,见链接,入队出队的时间复杂度均为 O(logn)。
优先队列实例见下:
1
| let q = new PriorityQueue({ comparator: function(boarda, boardb) { return boarda.eval - boardb.eval; }});
|
该优先队列中存放的是 Board 对象,对象包含九宫格状态state、估值 eval、当前局面的哈希值 hashVal,如下所示:
1
2
3
4
5
6
| function Board(array, curStep) {
this.state = copy(array);
this.eval = evalute(curStep);
this.hashVal = _hash();
}
|
在进行搜索时,估值 eval 小的 Board 对象先出队,找到其九宫格状态 state 中空格的位置,对空格四个方向进行遍历得到合法的新的九宫格,通过 Map_dis 判断该状态(哈希值)是否访问过并记录该状态(哈希值)下已走的最小步数。此外,为了得到求解方案,还需一个 Map_pre 记录该状态(哈希值)的前一个状态(哈希值)。
A∗算法核心代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| function aStar(sx, sy, solution) {
let startBoard = new Board(startArray, 0);
let endBoard = new Board(endArray, 0);
let dx = [0, 1, 0, -1], dy = [1, 0, -1, 0];
let dis = new Map(), pre = new Map();
let q = new PriorityQueue({ comparator: function(boarda, boardb) { return boarda.eval - boardb.eval; }});
q.queue(startBoard);
dis.set(startBoard.hashVal, 0);
while (q.length > 0) {
let curBoard = q.dequeue();
let curS = getSpacePos(curBoard);
if (curBoard.hashVal == endBoard.hashVal) {
getSolution(pre, endBoard.hashVal, solution);
console.log("search Finished!");
return dis.get(curBoard.hashVal);
}
for (let dir = 0; dir < 4; dir++) {
let nx = curS.x + dx[dir], ny = curS.y + dy[dir];
if (nx < 0 || nx > 2 || ny < 0 || ny > 2) continue;
curBoard.swap(curS.x, curS.y, nx, ny);
let nxtBoard = new Board(curBoard.state, dis.get(curBoard.hashVal));
if ((dis.get(nxtBoard.hashVal) == undefined) || dis[nxtBoard.hashVal] > dis[curBoard.hashVal] + 1) {
dis.set(nxtBoard.hashVal, dis.get(curBoard.hashVal) + 1);
pre.set(nxtBoard.hashVal, curBoard.hashVal);
q.queue(nxtBoard);
}
curBoard.swap(curS.x, curS.y, nx, ny);
}
}
console.log("search Finished!");
return -1;
}
|
当搜索到出队元素的状态(哈希值)等于目标状态(哈希值)时,表明已找到最优解,调用编写的 getSolution 函数得到路径,并返回最优解的步数。对于路径求法,简单地来讲就是从目标状态(哈希值)开始,不断求 Map_pre(hashVal) 值,并插入到可变长数组 Array 末尾。这样只要对比数组相邻两个元素之间空格位置的差异,就可以求出移动方案。
1
2
3
4
5
6
7
8
9
| function getSolution(pre, endHash, solution) {
let curHashVal = endHash;
while (curHashVal != undefined) {
let tmp = curHashVal.toString();
if (tmp.length != 9) tmp = "0" + tmp;
solution.push(tmp);
curHashVal = pre.get(curHashVal);
}
}
|
当队列为空且仍未找到解时,返回 -1,之后再通过界面进一步交互。当然,未找到解的情况会耗费很多不必要的资源和时间,如果能在求解前能判断有没有解,能进一步提高程序效率,这也将在后面优化部分介绍。
上述算法得到的 javascript 程序和已有标准 c++ 程序对拍无误,能够在毫秒时间内求解。当然依旧有优化的空间,将在后面优化部分介绍。
界面设计与结果演示
1.界面设计

九宫格如上图所示,分为起始状态九宫格和目标状态九宫格。每个九宫格分为背景和 9 个 input 格子,9 个格子分为 3 行,并赋予 id。通过 css 实现三行对齐排列并进行美化。
起始状态九宫格中的数字需要自己输入,目标状态的九宫格中填充了默认八数码问题目标状态,当然也可以自己进行修改。输入的数码不要求正确,因为在进行求解前会判断不合法的输入,并通过 window.alert() 提示错误信息。
九宫格 html 代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| <div class="center board">
<div id="srow1" class="input-row1">
<input type="text" id="s1">
<input type="text" id="s2">
<input type="text" id="s3"><br>
</div>
<div id="srow2">
<input type="text" id="s4">
<input type="text" id="s5">
<input type="text" id="s6"><br>
</div>
<div id="srow3">
<input type="text" id="s7">
<input type="text" id="s8">
<input type="text" id="s9"><br>
</div>
</div>
|
除此之外,还设置了 4 个交互按钮如下:
1
2
3
4
5
6
| <div class="center button-wrapper">
<button id="inputs-button">清空初态</button>
<button id="inpute-button">清空末态</button>
<button id="calc-button">求解</button>
<button id="reset-button">重置</button>
</div>
|
其中清空初始状态、清空末状态按钮以及重置按钮便于重新设定数码。前两个清空按钮在求解演示时不能使用,重置按钮在求解演示时选择性重置,以便立即结束求解演示重新布置数码。如下图所示:


对于求解按钮,点击后会先调用判断函数判断输入是否合法,然后进行初始化操作,求出方案,再调用演示函数进行结果演示。

此外,在界面右端还有一个显示剩余步数的文本,随演示进行而变化。
1
| <p class="step-paragraph">距离最终状态还需 <p1 class="step-num" id="step-num">?</p1> 步</p>
|
求解成功和失败界面:


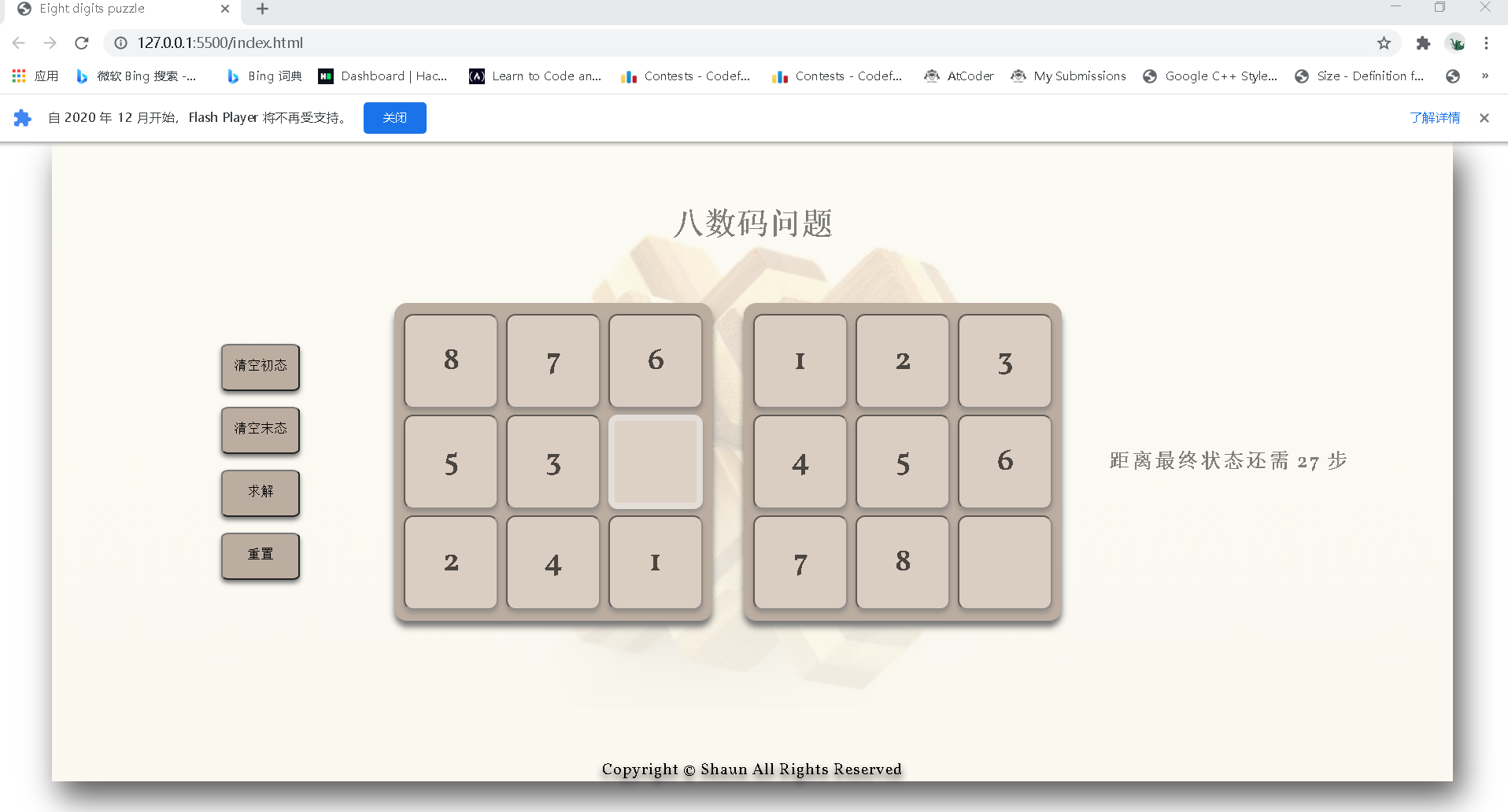
2.结果演示
在第一部分算法设计中已提到,求解得到的路径已存放在可变长数组中。接下来就只需从后往前找到数组相邻两个元素的空格的位置。由于已设定好九宫格每个格子的 id 以及所在的行的 id,所以通过空格的位置可以很方便地求得其所对应的 html 节点。
最后,通过 javascript 对 DOM 的一系列操作和计时事件即可在前端显示出空格每隔一段时间移动的效果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| async function displaySolution(solution) {
document.getElementById("step-num").innerHTML = solution.length - 1;
if (solution.length <= 1) {
running = false;
setTimeout(() => {
successMsg("求解完成!");
}, 1000);
return;
}
(function myLoop(i) {
setTimeout(() => {
document.getElementById("step-num").innerHTML = i - 1;
let id1 = "s" + (solution[i].indexOf("0") + 1);
let id2 = "s" + (solution[i - 1].indexOf("0") + 1);
let node1 = document.getElementById(id1);
let node2 = document.getElementById(id2);
let new1 = document.createElement("input");
new1.type = "text";
new1.id = id1;
new1.value = node2.value;
let new2 = document.createElement("input");
new2.type = "text";
new2.id = id2;
new2.value = node1.value;
new2.style.cssText = node1.style.cssText;
let faId1 = "srow" + (Math.floor(solution[i].indexOf("0") / 3) + 1);
let faId2 = "srow" + (Math.floor(solution[i - 1].indexOf("0") / 3) + 1);
document.getElementById(faId1).replaceChild(new1, node1);
document.getElementById(faId2).replaceChild(new2, node2);
if ((--i) >= 1) myLoop(i);
else {
running = false;
setTimeout(() => {
successMsg("求解完成!");
}, 1000);
}
}, 1000);
})(solution.length - 1);
}
|
算法优化
1. 无解判断
前面提到如果在 A∗ 算法搜索过程中,如果优先队列为空时仍然未找达到最终状态,则无解。但这会遍历所有可能的状态直至队列为空,空间与时间的消耗较大。如果在求解前进行判断,将会提高无解情况下的效率。
八数码两个局面可达,当且仅当局面下网格中的数依次写成 1 行 n2−1 个元素时,逆序对个数的奇偶性相同。该性质的必要性很容易证明:空格左右移动时,写成的序列显然不变;空格上(下)移动时,相当于某个数与它后(前)的 2 个数交换位置,逆序对数变化是偶数。充分性证明较复杂,就不在此大篇幅讨论这样的一个数学问题。
2. 康托展开
前面使用的是 Map() 存储简单哈希值,效率偏低。但如果使用康托展开,则可以对全排列进行编码和解码,把 1~N 的前排列与 1~N! 之间的整数建立一一映射关系。这样就可以 O(1) 时间得到一个状态的信息。
3. IDA*
$A^* $ 算法有一个显而易见的缺点,就是需要维护一个优先队列来存储状态以及估价,耗费空间较大,并且对优先队列进行依次操作也要花费 O(logn) 的时间。$IDA^* $ 以迭代加深 DFS 的搜索框架为基础,即限定一个深度,在不超过该深度的前提下执行 DFS,并把原来的简单的深度限制加强为:若当前深度 + 未来估计步数 > 深度限制,则立即从当前分支回溯。若找不到解,则扩大搜索深度,重新进行搜索。
事实证明 $IDA^* $ 效率要优于 $A^* $,且程序实现难度低于 A∗。
使用说明
双击打开 index.html 文件即可(建议使用 Chrome、FireFox 等浏览器),在输入起始状态和目标状态后点击求解按钮即可进行求解并演示方案。
项目github地址。